505, Mathématiques et langue française, Le 17 décembre 2018

01. Ensembles et sous-ensembles

Enoncé

On souhaite décomposer l’ensemble (2, 3, …, 32) en sous-ensembles vérifiant qu’aucun de ses éléments ne divise les autres.

Compter le nombre minimal de sous-ensembles nécessaires afin que cela soit possible.

Calcul

Dans l'ensemble complet {2, 3, … , 33} le facteur premier 2n est beaucoup représenté. On a ainsi une liste de nombres qui ne doivent absolument pas se trouver ensemble. Jusqu’à 33 on a {2, 4, 8, 16, 32}. On peut donc déjà dire qu’il y aura au minimum 5 sous-ensembles. Reste à voir si on peut caser tous les autres éléments dans chacun de ces 5 sous-groupes. Par exemple :

Dans le groupe qui contient 32, on peut mettre : 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33
Dans le groupe du 16 : 9, 10, 11, 12, 13, 14, 15, 16
Dans le groupe du 8 : 5, 6, 7, 8
Dans le groupe du 4 : 3, 4
Le 2 reste tout seul : 2

Résultat

Le nombre minimal de sous-ensembles est 5.

02. Est-ce bien logique ?

Enoncé

Cet exercice est une sensibilisation aux différents articulateurs logiques (cause, conséquence, hypothèse, condition, déduction…) éléments de cohérence textuelle.

Consigne : certaines des phrases suivantes sont absurdes ! Procéder aux changements qui permettent de leur donner du sens.

  1. Il est revenu dans son village après 20 ans d’absence et il a tout reconnu : la vieille gare avait été détruite pendant la guerre, l’église avait été modernisée avec d’affreux clochetons en stuc et le café de la place avait été remplacé par une pompe à essence.
  2. Le printemps arrive entraînant orages, pluies et premières chutes de neige. Toute la nature se prépare au repos.
  3. Au jour du Jugement Dernier, si tes bonnes actions pèsent plus lourd que tes mauvaises actions, alors tu iras dans les flammes de l’enfer.
  4. La conclusion de toutes ces années de recherche, c’est qu’il n’a rien trouvé et que par conséquent il a reçu le Prix Nobel.
  5. Sous l’effet du choc, il a été capable de dire son nom et d’expliquer ce qu’il faisait là à trois heures du matin.

Correction des phrases.

1. … il a tout reconnu … … après 20 ans d’absence, Il n’a pas reconnu : la vieille gare …
2. le printemps … L’automne arrive entrainant orages, …
3. … bonnes … mauvaises … , si tes mauvaises actions pèsent plus lourd que tes bonnes actions …
4. … il a reçu … … et que par conséquent il n’ a pas reçu le prix Nobel.
5. … capable … … , il a été incapable de dire son nom …

03. Marqueurs de cause

Enoncé

a) Les marqueurs de cause sont très fréquents dans le discours scientifique.

Consigne : complétez les phrases suivantes :

  1. . . . son grand âge, je n’ai rien dit, mais je n’en pensais pas moins !
  2. . . . grives, on mange des merles. / . . . d’argent ou de chance, on doit se contenter de peu.
  3. . . . la colère, il a cassé une vitre.
  4. Il ne viendra pas . . . il n’est pas très courageux.
  5. . . . il ne va pas en Chine, c’est qu’il ne parle pas le chinois.
  6. . . . du brusque changement de température, les bourgeons ne sont pas sortis.
  7. . . . elle adore les enfants et qu’elle ne peut pas en avoir, elle en a adopté trois !
  8. . . . tu m’aimes, marions-nous !
  9. Les deux forces s’annulent. . . du principe d’interaction.

b) Sensibilisation aux différents marqueurs de la cause.

Consigne : dans les phrases suivantes, repérez les différents marqueurs de la cause.

  1. Le nombre d’accidents mortels provoqués par les conducteurs en état d’ivresse a encore augmenté cette année.
  2. Pour cause départ, vends Mercedes 220 SE moins de 50 000 km.
  3. Le boa est parti au zoo. A la suite de plaintes réitérées de plusieurs voisins, inquiets de croiser régulièrement un boa en liberté dans l’escalier, le tribunal de Saint-Martin-d’Hères a obligé le propriétaire du reptile à placer son animal dans un zoo.
  4. Cinq personnes ont été hospitalisées pour intoxication alimentaire. En effet, elles avaient toutes les cinq mangé du jambon avarié.
  5. « En vertu des pouvoirs qui nous sont conférés, nous vous déclarons unis par les liens du mariage ».
  6. C’est un billet de la loterie nationale qui est à l’origine de sa fortune et de son ascension sociale.
  7. Je ne suis pas venu en cours, non pas parce que le sujet ne me plaisait pas, mais parce que j’étais parti en voyage.
  8. Il a proposé ses services à la mafia, poussé par l’esprit de vengeance et la cupidité.

a, Phrases complétées

  1. Etant donné son grand âge, …
  2. Faute de grives, on mange des merles. Par manque d’argent …
  3. Sous l’effet de la colère, …
  4. Il ne viendra pas car il n’est …
  5. S’il ne va pas en Chine, c’est qu’il …
  6. En raison du brusque changement de température …
  7. Comme elle adore les enfants et qu’elle …
  8. Puisque tu m’aimes, marions-nous !
  9. Les deux forces s’annulent à cause du principe …

b, Marqueurs de cause repérés

  1. … provoqués par les conducteurs …
  2. Pour cause départ, vends …
  3. … au zoo. A la suite de plaintes …
  4. … hospitalisées pour intoxication alimentaire. …
  5. « En vertu des pouvoirs qui nous sont … »
  6. … loterie nationale qui est à l’origine de sa fortune …
  7. … ne me plaisait pas, mais parce que j’étais parti …
  8. … ses services à la mafia, poussé par l’esprit de …

04. Cheval, vache et mouton

Enoncé

Un agriculteur a du foin pour nourrir un cheval, une vache et un mouton. Avec ce qu’il a, il peut nourrir le cheval et la vache pendant 12 mois, la vache et le mouton pendant 15 mois, ou encore le cheval et le mouton pendant 20 mois.

Pendant combien de temps peut-il nourrir les trois animaux ensemble ?

Calcul

Soit la quantité de foin disponible x
Soit les quantités de foin consommés en un mois c (par le cheval), v (par la vache) et m (par le mouton)
Le cheval et la vache consomment ensemble 12 (c + v) = x c + v = x / 12
La vache et le mouton consomment ensemble 15 (v + m) = x v + m = x / 15
Le cheval et le mouton consomment ensemble 20 (c + m) = x c + m = x / 20
2 (c + v + m) = (5x + 4x + 3x) / 60
120 (c + v + m) = 12x x = 10 (c + v + m)

Résultat

Les trois animaux ensemble peuvent manger pendant 10 mois

05. Lien entre texte et figure

Enoncé

. . .

a. Faire une figure représentant chacune des situations géométriques suivantes :

  1. « Soit un triangle ABC, un point M de [AB] et un point N de [AC], tel que (MN)//(BC) ».
  2. « Soit un triangle ABC et une droite (MN) parallèle à (BC). Le cercle de centre A passant par N coupe (AC) en P ».
  3. « Soit ABC un triangle. D, E et F désignent les milieux respectifs de (BA), (AC) et (CB). Les parallèles à (AF) menées par D et E coupent (BC) en G et H ».

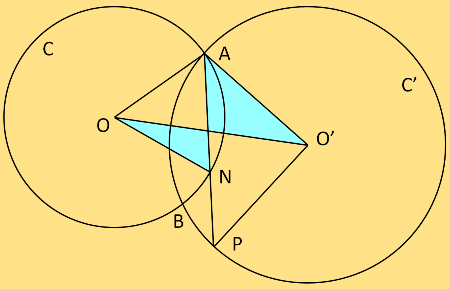
b. Observez la figure ci-contre et répondez par VRAI ou FAUX aux affirmations ci-après.

  1. Le cercle C a pour centre le point A
  2. Les cercles C et C’ n’ont aucun point en commun.
  3. Le triangle AON est isocèle.
  4. Le point B appartient aux deux cercles C et C’.
  5. Le triangle AO’P est isocèle.

Figures de la question a

. . .

Affirmations de la question b

  1. Faux, le centre du cercle C n’est pas le point A. Son centre est O.
  2. Faux, les deux cercles C et C’ ont les points A et B communs.
  3. Vrai, le triangle AON est isocèle. OA et ON sont égaux (deux rayons d’un même cercle).
  4. Vrai, le point B appartient aux deux cercles C et C’.
  5. Vrai, le triangle AO’P est isocèle. O’A et O’P sont les rayons d’un même cercle.

06. Multiples de 7

Enoncé

a k b =
7k - 10a 		10a + b x
a - 2b
1 1 -3 7 7
1 2 4 14 -7
3 5 5 35 -7
3 4 -2 28 7
3 3 -9 21 21
7 3 -49 21 105

Si 10a + b est un multiple de 7, a – 2b est-il un multiple de 7 ?

Calcul

Si 10a + b est multiple de 7, alors (avec k un entier) 10a + b = 7k 20a + 2b = 14k
Avec a – 2b = x 21a = 14k + x
x = 21a – 14k x = 7 (3a – 2k)

Résultat

x, c'est à dire [a – 2b], est toujours un multiple de 7. Voir quelques vérifications numériques à droite.

07. La belote

Enoncé

L’objectif de cet exercice est d’apprendre à sélectionner, dans une masse d’informations, celles qui sont pertinentes pour permettre d’atteindre le but recherché. En l’espèce, il conviendra de sélectionner, dans une liste d’informations, les éléments nécessaires pour remplir une grille.

Consignes :

  1. Remplir la grille ci-dessous à l’aide des informations données dans la liste ci-dessous. Il faudra relire la liste au fur et à mesure que vous remplirez la grille.
  2. Justifier la démarche suivie ainsi que les réponses.

Les données :

A la belote, les joueurs sont opposés deux à deux (Nord et Sud sont partenaires et adversaires d’Ouest et Est). L’expression « A main droite » désigne le joueur le plus près de la main droite. Ainsi, à main droite de « Nord » se trouve « Ouest ». Dans le jeu qui nous concerne, il y a, par ordre alphabétique !

Informations :

Grille :

Position Nord Est Sud Ouest
Prénoms
Professions
Qualités
Défauts
Loisirs
  1. Celui qui joue au foot a pour adversaire le médecin et Orlando.
  2. Le partenaire de Mohamed est généreux, mais il n’est pas patient.
  3. A main droite du médecin, il y a le physicien.
  4. Peter n’aime pas le ski.
  5. Orlando est entre le physicien et Mohammed.
  6. Celui qui est au Nord est physicien et n’a pas Peter pour partenaire.
  7. L’informaticien fume trop ce qui le gêne pour pratiquer son sport favori : le foot.
  8. Le partenaire du physicien joue au foot.
  9. Un des adversaires de Mohamed est très bavard mais très patient.
  10. Celui qui fait du vélo est assis en face de Peter.
  11. Le médecin est patient.
  12. Celui qui fait du vélo est très amusant.

Calcul et Résultat

Nord Est Sud Ouest
Les amis : J, M, O, P k : Jacques k: Peter a : pas Peter
e: Mohamed 		d : Orlando
Professions : A, I, M, P a : Physicien c : Médecin f : Informaticien f : Agronome
Qualités : A, G, P, S g : Généreux h : Patient m : Souriant m : Amusant
Défauts : B, C, F, I g : Impatient i : Bavard f : Fumeur l : Coléreux
Loisirs : F, S, T, V l : Ski l : Tennis b : Foot j : Vélo

08. Pythagore

Enoncé

. . .
. . .

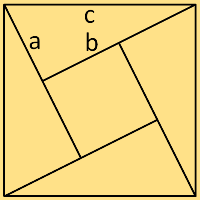
a) Voir à droite une première figure géométrique. En vous aidant de cette figure, rédigez une démonstration du théorème de Pythagore. (Pour cela, il sera utile d’utiliser les formules donnant la surface d’un carré et celle donnant la surface d’un triangle rectangle).

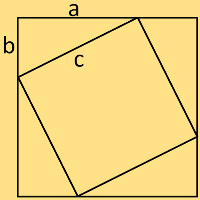
b) Les mathématiciens indiens donnèrent, vers 1 200 après J.C. une autre démonstration du théorème de Pythagore basée sur la deuxième figure de droite. Retrouvez cette démonstration.

Démonstrations

Aire du grand carré (première figure) (a + b)2 = a2 + 2ab + b2
Aire des 4 triangles rectangles 4ab/2 = 2ab
Aire du carré central = le grand – les 4 triangles rectangles a2 + 2ab + b2 – 2ab = a2 + b2 = c2
D’où la relation de Pythagore c2 = a2 + b2
Aire du petit carré (deuxième figure) (b – a)2 = a2 – 2ab + b2
Aire des 4 triangles rectangles 2ab
Grand carré = le petit + les 4 triangles rectangles a2 – 2 ab + b2 + 2ab = a2 + b2 = c2
c2 = a2 + b2

09. Absurde, vous avez dit absurde !

Enoncé

Personnage Arthur Philippe Pierre Claude François
Nature (Ange ou diable)
Ce qu'il dit
Déduction

On propose, ici, un raisonnement par l’absurde sur la base du jeu suivant :

1. En utilisant un raisonnement par l’absurde, montrez que Arthur est un diable. Vous pourrez, pour cela, vous appuyer sur le tableau ci-contre.

2. Sachant que Arthur est un diable, déterminez qui est ange et qui est diable.

Calcul

Avec l'hypothèse : Arthur est ange avec l'hypothèse : Arthur est diable
Personnage Arthur Philippe Pierre Claude François Arthur Philippe Pierre Claude François
Statut d'Arthur donné par l'hypotèse A D
Arthur dit : "Philippe est diable", donc : D A
Philippe dit : "Pierre est ange", donc D A
Pierre dit : "Claude est diable", donc A D
Claude dit : "François est ange", donc A D
Pour François, Arthur et Philippe sont tous les deux diables D D
Résultat Contradictoire, l'hypothèse est fausse. C'est faux, donc l'hypothèse est la bonne.

Résultat

Arthur est Diable, Philippe est Ange, Pierre est Ange, Claude est Diable et François est Diable.

10. Questions simples

Enoncé, Calculs et Résultats

N° Enoncé Calcul Résultat
Aa Thomas numérote quatre jetons : 2, 3, 4 et 6. Placez les jetons sur les cases vides pour que le résultat soit 38. ꙱꙱ / ꙱ + (5 x ꙱) = 38. 36 / 2 + 5 x 4 = 38
Ab Je suis un nombre qui a trois voyelles et trois consonnes. J’ai un Q, mais pas de T. Qui suis-je ? Je suis le nombre QUINZE.
Ac Antoine écrit 15 fois le nombre 7 et introduit le signe de multiplication entre les 7. Quel sera le dernier chiffre du résultat ? 715 = (75)3
71 72 73 74 75 710 715
Ch des un. 7 9 3 1 7 9 3
Vérification : 715 = 4 747 561 509 943 		Le dernier chiffre de 715 est 3.
Ad De combien d’allumettes a-t-on besoin pour dessiner une grille rectangulaire 4 x 5 ? 1 fois ----- + 4 fois |-|-|-|-|-|
= 4(6 + 5) + 5 = 49 		Il faut 49 allumettes.
Ba Combien y a-t-il de jours de la semaine dont le mot contient un seul D ? Vendredi s'écrit avec 2 D, il reste Six jours de la semaine avec un seul D.
Bb Vrai ou faux. Le rayon d'un cercle est aussi appelé corde. Non, la corde doit rejoindre
un autre point du cercle.
Bc La somme de deux nombres est 80. Le double du plus petit est 72. Quel est le plus grand ? Soit x le plus grand. 2 (80 – x) = 72 ; x = 44 Ce nombre est 44.
Bd À quel nombre vous fait penser le mot TÉTRAPODE ? Le mot tétrapode fait penser
au nombre 4.
Be Combien y a-t-il de jours dans le quatrième trimestre d’une année ? 31 + 30 + 31 = 92 Le quatrième trimestre d’une année a 92 jours.
Bf Marc a six dés. Il en reçoit deux fois plus qu'il en a. Combien Marc a-t-il de dés maintenant ? 6 (1 + 2) = 18 Marc a maintenant 18 dés.
Bg Quel est le quantième de mai qui est le 50e jour du deuxième trimestre d’une année ? Avril a 30 jours ; 50 – 30 = 20 Ce jour est le 20 mai.
Bh Quel est le reste de la division de 53 par 7 ? 53 = 7 x 7 + 4 Le reste de la division est 4.
Bi En retranchant 62 à un nombre, on obtient 26. Quel est ce nombre ? 26 + 62 = 88 Ce nombre est 88.
Bj Sur un cadran en papier, une aiguille est sur le 2 et l’autre sur le 7. Quelle est la mesure du plus petit angle formé par les deux aiguilles ? 360 [(7 – 2) / 12] = 150 Les aiguilles font un angle de 150°.

11. L’âge d’Anna

Enoncé

En multipliant l’âge d’Anna par 6 puis en retranchant 6, on obtient le même nombre qu’en retranchant 7 à l’âge d’Anna et en multipliant le résultat par 7.

Quel est alors l’âge d’Anna ?

Calcul

6x – 6 = 7(x – 7) 7x – 6x = 49 – 6 x = 43

Résultat

Anna a 43 ans.

12. Jeux et probabilités

Enoncé

Lisez le texte suivant : « Considérons un jeu de hasard consistant à lancer un dé. Le lancer du dé est une épreuve. Il y a six résultats possibles puisque le dé comporte six faces. Chacun des résultats possibles est un événement élémentaire (ou éventualité). Remarque : les événements élémentaires s’excluent mutuellement. Dans l’exemple, le dé ne peut retomber sur deux faces à la fois.

Si le dé est homogène et symétrique, les six événements élémentaires sont également probables (ou équiprobables). La probabilité de chacun des six événements élémentaires est égale à 1/6. D’une manière générale, soit l’ensemble des n événements élémentaires équiprobables susceptibles de résulter d’une épreuve : la probabilité d’un événement élémentaire équiprobable est égale à 1/n.

Soit E l’ensemble des événements élémentaires relatifs à une épreuve. Par exemple, pour l’épreuve du lancer d’un dé : E = {1, 2, 3, 4, 5, 6}. Un événement est un sous-ensemble de E. Ainsi, si A est l’événement « obtenir un résultat pair », A = {2, 4, 6}. Soit n le nombre des événements élémentaires équiprobables possibles, susceptibles de résulter d’une épreuve ; soit k le nombre des événements élémentaires qui sont favorables à un événement A donné résultant de cette épreuve, la probabilité de l’événement A et égale à k/n.

Répondre aux questions suivantes :

  1. Lors d’une épreuve consistant à tirer au hasard une carte parmi un jeu de 52 cartes, les évènements élémentaires sont-ils équiprobables ?
  2. Un événement peut être qualifié de certain ou d’impossible. Quelle est la probabilité d’un événement certain ?
  3. Quelle est la probabilité d’un événement impossible ?
  4. VRAI ou FAUX ?

Réponses

  1. Oui, au cours du tirage d’une carte dans un jeu de 52, les évènements élémentaires sont équiprobables.
  2. Evènement certain ou impossibe,
  3. Vrai ou faux

13. William Wilson

Enoncé

S E N D
+ M O R E
= M O N E Y

William Wilson est un jeune étudiant en mathématiques. Plus brillant qu’assidu, il fréquente les cabarets plus que les bibliothèques. Il y joue beaucoup d’argent et, malgré son indéniable talent dans le domaine des probabilités, il en perd souvent. Il est donc fréquemment appelé à écrire à ses parents pour leur demander de lui envoyer de l’argent. Sa dernière lettre, laconique, est ainsi libellée : (voir ci-contre)

Quel est le montant de la somme que William Wilson demande à ses parents ?

Calcul

r4 r3 r2 r1
S E N D
+ M O R E
= M O N E Y

Il y a une solution principale plus 24 autres solutions secondaires dans lesquelles deux des nombres commencent par un zéro. Quelques relations permettent d’éliminer les combinaisons qui ne conviennent pas.

1. La retenue r4 est égale à M M vaut 0 ou 1. De même toutes les retenues r1 à r3 valent 0 ou 1
2. Colonne des milliers r3 + S + M = O + 10M O = S – 9M + r3
3. Colonne des centaines r2 + E + O = N + 10r3 E = N – O + 10r3 – r2
4. Colonne des dizaines r1 + N + R = E + 10r2 R = E – N + 10r2 – r1
5. Colonne des unités D + E = Y + 10 r1 Y = D + E – 10r1
Egalité r1 r2 r3 M O S E N R Y D Observation
Prendre M = 1 ; O - S = r3 - 9 0 1 0 9
1 1 1 9 Non, 1 est déjà pris
1 1 0 8
E - N = 10r3 - r2 - O 0 0 1 0 9 Non, entraine E = N
1 0 1 0 9 7 8
1 0 1 0 9 6 7
1 0 1 0 9 5 6
1 0 1 0 9 4 5
1 0 1 0 9 3 4
1 0 1 0 9 2 3
0 1 1 0 8 Non, entraine E - N = 10
1 1 1 0 8 7 6
1 1 1 0 8 6 5
1 1 1 0 8 5 4
1 1 1 0 8 4 3
1 1 1 0 8 3 2
R = E - N + 10r2 - r1 0 1 0 1 0 9 7 8 9 Non, R = 9 dans toute la série, 9 déjà pris
1 1 0 1 0 9 7 8 8 Non, R = 8, déjà pris
1 1 0 1 0 9 6 7 8
1 1 0 1 0 9 5 6 8
1 1 0 1 0 9 4 5 8
1 1 0 1 0 9 3 4 8
1 1 0 1 0 9 2 3 8
0 1 1 1 0 8 7 6 Non, R = 11 pour toute la série
1 1 1 1 0 8 7 6 Non, R = 10 pour toute la série
Y - D = E - 10r1 1 1 0 1 0 9 6 7 8 2 6 Non, D = 6 déjà pris
1 1 0 1 0 9 6 7 8 3 7 Non, D = 7 déjà pris
1 1 0 1 0 9 6 7 8 4 8 Non, D = 8 déjà pris
1 1 0 1 0 9 6 7 8 5 9 Non, D = 9 déjà pris
1 1 0 1 0 9 5 6 8 2 7 C'est la solution.
1 1 0 1 0 9 5 6 8 3 8 Non, D = 8 déjà pris
1 1 0 1 0 9 5 6 8 4 9 Non, D = 9 déjà pris
1 1 0 1 0 9 4 5 8 2 8 Non, D = 8 déjà pris
1 1 0 1 0 9 4 5 8 3 9 Non, D = 9 déjà pris
1 1 0 1 0 9 3 4 8 2 9 Non, D = 9 déjà pris
1 1 0 1 0 9 2 3 8 Non, entraine l'utilisatin de chiffres déjà utilisés
9 5 6 7
+ 1 0 8 5
= 1 0 6 5 2

Les autres solutions

2 817 + 0 368 = 03 185 5 731 + 0 647 = 06 378 6 853 + 0 728 = 07 581 7 534 + 0 825 = 08 359
2 819 + 0 368 = 03 187 5 732 + 0 647 = 06 379 6 851 + 0 738 = 07 589 7 649 + 0 816 = 08 465
3 719 + 0 457 = 04 176 5 849 + 0 638 = 06 487 7 316 + 0 823 = 08 139 7 643 + 0 826 = 08 469
3 712 + 0 467 = 04 179 6 419 + 0 724 = 07 143 7 429 + 0 814 = 08 243 8 324 + 0 913 = 09 237
3 829 + 0 458 = 04 287 6 415 + 0 734 = 07 149 7 539 + 0 815 = 08 354 8 432 + 0 914 = 09 346
3 821 + 0 468 = 04 289 6 524 + 0 735 = 07 259 7 531 + 0 825 = 08 356 8 542 + 0 915 = 09 457

14. Pour cinéphiles avertis

r3 r2 r1
F I L M
+ C I N
+ E M A
= A I M E

Enoncé

Chaque lettre représente un chiffre différent. Indices : N = 5 et E = 8.

Déchiffrez cette addition. (Il y a quatre dispositions possibles).

Calcul

r3 0 0 0 1 1 1 2 2 2
r2 0 1 2 0 1 2 0 1 2
C -8 -9 -10 2 1 0 12 11 10
Etant donné la présence de trois lignes dans l’addition, les retenues r1, r2, r3 peuvent être 0, 1 ou 2.
Colonne des centaines, avec E = 8 r2 + I + C + 8 = I + 10r3 C = 10r3 – r2 – 8
Suivant les valeurs de r3 et r2 Les cellules sur fond gris sont interdites, prendre les jaunes.
r1 0 1 2
A 3 - M 13 - M 23 - M
Voir A = f(M), colonne des unités M + 5 + A = 8 + 10r1 A = 3 – M + 10r1



r3 0 1 2
F A A - 1 A - 2
Voir F = f(A), colonne des milliers r3 + F = A F = A – r3



r3 0 0 0 1 1 1 2 2 2
r2 0 1 2 0 1 2 0 1 2
I -L -L - 1 -L - 2 10 - L 9 - L 8 - L 20 - L 19 - L 18 - L
Voir I = f(L), colonne des dizaines r1 + L + I + M = M + 10r2 I = 10r2 – L – r1




r3 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
r2 0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 2 2 2
r1 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2
Domaines de validité des retenues




L 0 1 2 3 4 5 6 7 8 9
I = 10 - L 10 9 8 7 6 5 4 3 2 1
M 0 1 2 3
A = 3 - M 3 2 1 0
F = A - 1 2 1 0 -1
Avec r3 = 1, r2 = 1 et r1 = 0 C = 1 dans tous les cas




M 0 1 2 3 4 5 6 7 8 9
I = 9 - L 9 8 7 6 5 4 3 2 1 0
M 4 5 6 7 8 9
A = 13 - M 9 8 7 6 5 4
F = A - 1 8 7 6 5 4 3
Avec r3 = 1, r2 = 1, r1 = 1 C = 1 (toujours)
En définitive on a 4 solutions.


Résultat

F I L M 2 6 4 0 2 4 6 0 3 7 2 9 3 2 7 9
C I N 1 6 5 1 4 5 1 7 5 1 2 5
E M A 8 0 3 8 0 3 8 9 4 8 9 4
A I M E 3 6 0 8 3 4 0 8 4 7 9 8 4 2 9 8