Accueil
Bonjour et bienvenue vers la découverte de quelques curiosités "solaires".

Introduction
Objectif : faire un tour d'horizon sur l'histoire de la mesure du temps, le gnomon, les différents types de cadrans, l'équation du temps, la construction d'un cadran.
L'idée initiale était de montrer comment réaliser un cadran solaire avec le minimum de calculs par une construction géométrique soignée. Puis les réalisations de Zarbula ont été découvertes. On trouve la recette sur Internet.
| Le site de Michel Lalos | |
| La partie Zarbula du site de Michel Lalos | |
| Le fichier pdf de la recette, origine : Michel Lalos | |
|
| Le diaporama directement sur le site de Michel Lalos |
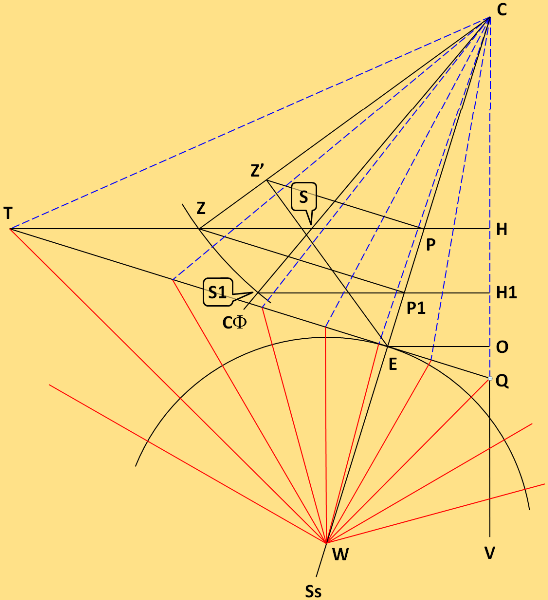
Voici un exemple de la construction géométrique de Zarbula. C'est spectaculaire et c'est juste.
Très sommairement, globalement (pour plus de détails, aller sur le site de Michel Lalos), pour reconstituer l'objet dans l'espace, il faut
plier :
- Le triangle CQE reste dans le plan de la table du cadran final.
- La figure CH1S1 est pliée autour de la ligne commune CH1, avec le projeté de CS1 sur CP1 (S1 à l'aplomb de P1). Donc pliage < à 90°.
- CP1Z doit être plié autour de CSs perpendiculairement au cadran.
- TQW est plié autour de TQ (d'un angle > à 90°), de manière à ramener le point W en Z'. Les deux points W et Z' se rejoignent au-dessus de la table.
- L'aiguille du cadran est CZ'.
Belle construction, mais on peut faire beaucoup plus simple en admettant d'utiliser la calculette un tout petit peu. Donc l'objectif est révisé : nous ferons une construction mixte basée sur ces principes :
- Acquisition expérimentale de la sous-stylaire CSs,
- Tracé des points caractéristiques à l'aide de formules simples (C, T, Q, W, H, P, E),
- Tracé géométrique des lignes horaires à partir du cadran équatorial (celui du plan TQW).
- Précisions sur la dimension et la position de l'aiguille.
Mais commençons par l'histoire et l'aperçu des principaux cadrans.
Sommaire
| Accueil | ||
|---|---|---|
| Introduction | ||
| Sommaire | ||
| Histoire de la mesure du temps | ||
| Astronomie et penseurs | ||
| Le calendrier autrefois | ||
| Repères de nos anciens dans le jour | ||
| Les différents appareils utilisés jadis pour la mesure de l'heure | ||
| Histoire et types de cadrans | ||
| Histoire de la mesure de l'heure avec le soleil | ||
| Le gnomon des anciens | ||
| Le cadran équatorial | ||
| Le cadran polaire | ||
| Les cadrans horizontaux et verticaux | ||
| Relations entre l'heure solaire et l'heure de la montre | ||
| Le méridien de référence, correction n° 1 | ||
| Correction n° 2, Equation du temps | ||
| Relation globale, Heure légale (de la montre) en fonction de l'heure solaire | ||
| Tables de la déclinaison terrestre et de l'Equation du temps | ||
| Construction d'un cadran solaire | ||
| L'homologue horizontal d'un vertical déclinant | ||
| Les outils, les mesures | ||
| Recherche de la sous-stylaire | ||
| Le dessin du cadran, méthode mixte | ||
| Quelques maximes rencontrées | ||
| Note finale |
Histoire de la mesure du temps
La mesure du temps et les besoins de précision évoluent dans le temps suivant un schéma semblable, parallèle, à celui de l’humanité et de ses ressources.
Il y a très longtemps, l’homme vivait de la cueillette et de la chasse. Puis il s’est mis à cultiver et à élever du bétail. L’abondance a entraîné une croissance de la population. Puis, la surpopulation a demandé d’améliorer les méthodes de culture et d’élevage ... etc.
Le calendrier et l’heure ont permis aux sociétés de s’organiser de mieux en mieux. Les marins ont eu besoin de « transporter » l’heure d’un méridien de référence, pour calculer la longitude au cours de leur progression et ne plus perdre de temps à errer dans leur navigation à l’estime. Les scientifiques ont besoin d’analyser des phénomènes de plus en plus rapides. A d’autres périodes, les progrès réalisés dans la mesure du temps leur ouvre la porte vers des champs d’investigation de plus en plus fins ... etc. Les moyens sont en avance ou en retard par rapport au besoin. Où est la limite du besoin ?
Astronomie et penseurs
Les phénomènes naturels, réguliers, les astres sont des repères de choix.
- Les Babyloniens et Egyptiens, les Incas, étaient d’excellents astronomes d’observation.
- Les treize constellations sont connues depuis 5000 ans : vierge – balance – scorpion – ophiucus – sagittaire – capricorne – verseau – poissons – bélier – taureau – gémeaux – cancer – lion.
- Sosigène d’Alexandrie (1er siècle avant Jésus Christ) apporte les éléments pour créer les années bissextiles.
- Nicolas Copernic (1473 – 1543) s’oppose à Ptolémé et fait passer le soleil au centre (par opposition au géocentrisme). L’idée demande un siècle avant d’être acceptée.
- Grégoire XIII (1502 – 1585), pape de 1572 à 1585 réforme le calendrier en 1582.
- Galilée dit Galiléo Galiléi (1564 – 1642) conçoit le pendule à la fin de sa vie.
- Johannes Kepler (1571 – 1630) aborde l’attraction universelle. Il établit les tables Rudolphines de position des astres en 1627.
- Christiaan Huygens (1629 – 1695) apporte le pendule et le balancier.
- Isaac Newton (1642 – 1727) précise la gravitation universelle et les lois sur les orbites elliptiques.
- Plusieurs nations organisent des concours en fin du 17ème, avec primes, pour la résolution du calcul de la longitude sur les bateaux.
- Ferdinand Berthoud (1727 – 1807) participe à la mise au point du chronomètre.
Le calendrier
- Début du monde, il y a 14 milliards d’années.
- Le calendrier de Babylone a été écrit par un prêtre, il y a 5000 ans.
- Puis le calendrier politique devient indépendant du calendrier religieux.
- L’année, le mois et le jour sont d’origine astrale. Tous sont incommensurables.
- Le calendrier Julien (Jules César) adopte l’idée de Sosigène ( - 30 ). L’apport des années bissextiles approche la réalité avec une erreur de 11 mn et 14 s par an.
- Le calendrier grégorien corrige 3 jours par 400 ans. Les années zéro de chaque siècle ne sont plus bissextiles, sauf une fois tous les 400 ans. L’année 2000 a été exceptionnellement bissextile. Les années 1900 et 2100 ne le sont pas.
- L’erreur résiduelle est de l’ordre de 1 jour par 3 millénaires.
- En 1582, il a fallu rattraper 10 jours de dérive. Ainsi, en France le dimanche 9 décembre 1582 a été suivi du lundi 20. Les jours du 10 au 19 décembre 1582 n’existent pas.
L'heure
- Pour les grecs et les romains et jusqu’au moyen âge, les heures sont de durée variable. Quelle que soit la saison, il y a 12 heures de nuit et 12 heures de jour.
- L’origine, le zéro de l’heure babylonique est au lever du soleil.
- L’origine de l’heure italique est au coucher.
- Les premiers appareils de mesure du temps sont déréglés pour les adapter à l’heure irrégulière.
- Mais les astronomes utilisent l’heure équinoxiale, constante, depuis l’antiquité.
- Une tentative de décimalisation de l’heure sous la Convention, 10 heures de 100 minutes, n’a vécu que quelques années.
- L’unité de temps de phénomènes rapides pour Galilée était le battement du pouls.
- Au 19ème siècle le temps de travail est compté en minutes, bien que les montres soient trop chères pour les ouvriers.
- En 1850 le télégraphe transmet l’heure de Paris aux gares.
- Les deux horloges des gares ont fonctionné longtemps ensemble : heure locale (du soleil) et heure de Paris.
- 1885 : au niveau mondial, les fuseaux horaires sont centrés sur le méridien international (ancien Greenwich). Paris refuse jusqu’à l’année 1911.
- 1916 : création de l’heure d’été : méridien de référence à –15°.
- 1933 : l’horloge parlante donne le temps universel coordonné (UTC).
- 1960 : les satellites donnent l’heure à la milliseconde près.
- 1960 : la seconde change de définition. Avant, il y avait 86400 secondes par jour solaire moyen. Après, c’est l’année solaire 1900, la référence, qui est divisée en (presque) 31 556 926 secondes (365 j, 5 h, 48 mn, 46s).
- 1967 : La seconde est définie par 9 192 631 770 vibrations du césium 133 à 10-13 près.
- Les pulsars sont aussi précis.
- 1976 : heure d’été et heure d’hiver – références aux longitudes de –30 et –15°.
Les appareils utilisés
- Le cadran solaire est l’appareil de base jusqu’à la fin du 19ème. Il sert à recaler quotidiennement tous les autres appareils.
- La clepsydre se sert du temps d’écoulement de l’eau par un orifice. Elle a été mécanisée jusqu’à faire de véritables horloges avec des figurines animées. La précision était évidemment très grossière et il fallait recaler sans cesse. L’eau a le désavantage d’être corrosive, volatile, et elle gèle dans les pays froids.
- Le sablier est adapté à des mesures de temps partiels très larges : la cuisson d’un œuf – la durée du quart sur un bateau ; mais aussi à la mesure d’un temps continu, transport de l’heure sur le bateau, à condition de le retourner régulièrement, sans attendre. Il est utilisé jusqu’au 19ème siècle. Il est moins cher et plus précis que la montre. Les marins avaient donné le nom d’ampoulettes à cet appareil.
- La cloche est le moyen d’information, de distribution de l’heure, et d’invitation à diverses actions, religieuses ou de travail, ou de transmission d’une alerte ...
- L’horloge à foliot du 13ème au 17ème est la première invention pure de l’homme. Dans cet appareil mécanique, le rythme est donné par le foliot, pièce à inertie très rudimentaire, à mouvement alternatif. C’est un levier lancé dans un sens, puis sauvagement bloqué et lancé dans l’autre sens.
- La deuxième aiguille de 60 minutes apparaît au 15ème.
- Vers le 16ème, la pendule et son pendule devient ce qu’on peut appeler une horloge.
- La montre avec son balancier à ressort de rappel, avec une moindre précision, permet de transporter l’heure.
- Au 17ème, la pendule atteint une précision de quelques secondes par jour et la montre 4 à 5 minutes par jour.
- Le chronomètre résout le problème de transport de l’heure avec une précision suffisante pour les marins. Il a fallu tout le 18ème siècle pour aboutir à ce résultat, avec des systèmes de compensation d’erreurs dues à la température, sur le balancier et par l’adoption de paliers en pierres (rubis).
- La montre à diapason de Bulova à 360 hertz était révolutionnaire en 1959. Son succès a été éphémère, à cause du quartz.
- Le quartz, taillé pour vibrer à 32 768 hertz (215) est largement connu. Aujourd’hui (en 2000), on produit dans le monde environ 500 millions de montres par an. A titre comparatif, on en produisait 1 million en 1900 et 100 000 en 1850. Révision de 2020 : 1,4 milliards de montres par an.
- L’horloge atomique donne la seconde avec la précision de la vibration du césium (10-13).
- Le balancier de Huygens a vécu près de 2 siècles.
- Dans le corps armé, au moyen âge, le soldat avait son réveil matin : le coq. Au 18ème l’officier avait sa montre. Une montre pour chaque soldat après la seconde guerre mondiale.

Les cadrans solaires
Histoire de la mesure de l'heure avec le soleil
- Les cadrans solaires sont inventés par les Egyptiens.
- Le cadran gréco-romain était sphérique, creux, conique, tronconique. Il y a un « Arachné » au Louvre.
- Au moyen âge, les cadrans canoniaux étaient événementiels : heure de la prière ...
- A la renaissance, le cadran polaire est utilisé.
- L’âge d’or de la gnomonique se situe aux 16 et 17ème. Les cadrans de hauteur, basés sur la hauteur du soleil, apparaissent : par exemple la montre de berger.
- Les 17 et 18ème voient le cadran armillaire se développer. C’est un cadran « équatorial » à bande.
- Le cadran analemmatique date de 1640 : François Vaulezard.
- Michnik invente le cadran bifilaire en 1922.
- Un recensement partiel :
- Hautes Alpes plus de 600
- Charente Maritime 500
- Paris 120
- Charente 80
- Les Landes 20
- L’alsace possède les plus anciens (XVème siècle).
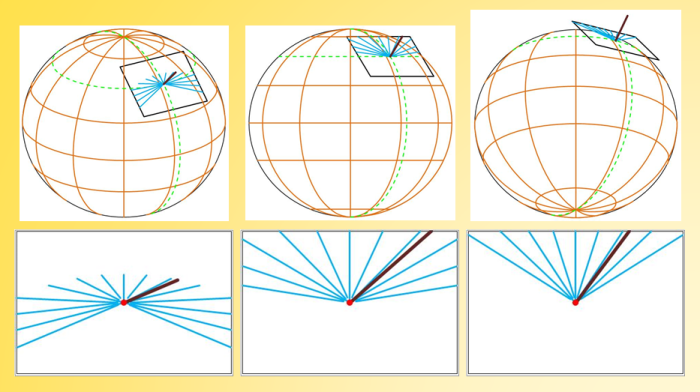
Le gnomon des anciens
Il est naturel de planter un bâton dans le sol et de regarder son ombre tourner autour. Sur le schéma de droite, la terre étant vue de face avec le soleil dans le dos, l'aiguille (le bâton) est superposée à l'ombre. A la latitude de 45° Nord, à 14h15 au soleil, l'ombre n'a pas du tout la même position suivant la déclinaison, c'est à dire à différentes dates de l'année. Cela obligerait à avoir des graduations différentes pour chaque jour.
Cependant, en isolant un disque équatorial qu'on fait tourner régulièrement autour de l'axe des pôles, on conçoit que, quelque soit l'orientation du disque face au soleil, les ombres progressent très régulièrement d'heure en heure, de 15 en 15°. C'est le secret : il faut que le bâton, le gnomon, l'aiguille, le style, soit parallèle à l'axe de rotation de la terre.
Le cadran équatorial
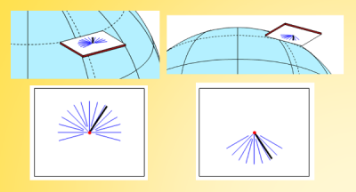
On peut installer un cadran équatorial à n'importe quelle latitude. C'est toujours le même dessin. Par contre, l'hiver il faut graduer la face inférieure du cadran, car le soleil est alternativement sur, ou sous, l'équateur.
Le cadran solaire équatorial est un cadran très facile à dessiner avec un trait tous les 15°. Il est plus difficile à positionner, car il faut que la table soit bien parallèle au plan équatorial terrestre.
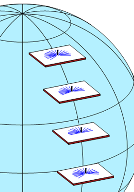
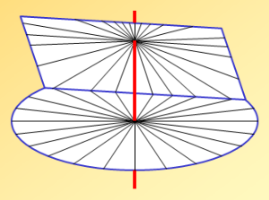
Plions maintenant le disque équatorial à 90°.
le cadran polaire
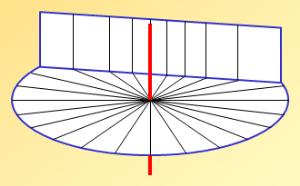
Le pliage donne un cadran solaire polaire. Sa table est parallèle à l'axe des pôles. L'aiguille est évidemment aussi parallèle à l'axe des pôles et elle ne rencontre jamais la table. Pour la graduation ce n'est pas difficile : on prolonge les traits horaires du cadran équatorial, à l'endroit de la pliure par des traits parallèles à l'aiguille, et donc parallèles entre eux.
Cette construction géométrique nous donne une idée de la méthode qu'on utilisera pour construire un cadran solaire horizontal ou vertical, à partir de la graduation du disque équatorial.
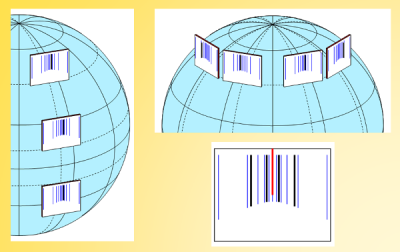
Les cadrans horizontaux et verticaux
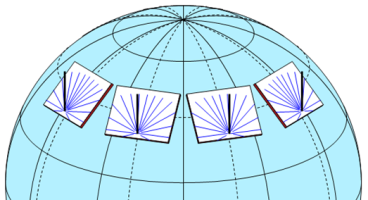
Il est naturel de chercher à construire localement, des cadrans au sol ou contre un mur. A condition de bien immobiliser l’aiguille dans sa position parallèle à l’axe des pôles, il est possible maintenant d’incliner le cadran équatorial, dans le sens Sud / Nord, dans le sens Est / Ouest, ou même dans les deux sens. L’image va se déformer, comme celle d’un projecteur face à un écran mobile. Il sera toujours possible de lire l’heure.
le cadran horizontal
A la latitude φ de 45°, l'aiguille est inclinée à 45° vers le nord.
Le cadran vertical plein sud
A la latitude φ de 45°, l'aiguille est toujours inclinée à 45° par rapport à la table, mais cette fois, vers le sud. Les méridiens tracés en traits pleins sont ceux des heures solaires paires (8, 10, 12, 14, 16 ...), c'est à dire des longitudes λ : 60, 30, 0, -30, -60° ... Les parallèles sont ceux des latitudes φ : 0 (équateur) ; 23,44 (tropique) ; 45 ; 66,56 (cercle polaire).

Un cadran vertical déclinant
Un mur n'est jamais parfaitement face au sud. Il est plus moins tourné vers l'Est ou l'Ouest. Le cadran de ce mur est appelé déclinant. Toujours pour la latitude φ de 45°, sur la terre de droite, le cadran est déclinant vers l’ouest. Sa table est exactement face au soleil à 14h30.
Il y a à observer sur la vue de ce cadran déclinant. Pour la déclinaison terrestre de 23,44°, correspondant au solstice d'été le 21 juin, la durée d’éclairage du cadran est diminuée. Par exemple le matin il fait jour, mais le cadran est éclairé par la face arrière. D’où la possibilité de faire un cadran orienté vers le Nord, avec des durées d’utilisation bien sûr très réduites. Le cadran est de profil à 9h28 et à 18h31.
Dessin des différents cadrans

On trouve de gauche à droite : l'équatorial, le polaire, l'horizontal, le vertical et le vertical déclinant.
Les couleurs sont utilisées pour la longueur de l'ombre :
- le bleu clair, au solstice d'hiver, le 22 décembre,
- le vert, à chacun des deux équinoxes, les 21 mars et 21 septembre,
- Couleur brique pour le solstice d'été, le 21 juin.
- Attention, il y a un défaut sur le cadran horizontal !
Dernière remarque : mis à part le pivotement, il y a une ressemblance entre le cadran vertical et le cadran vertical déclinant.
Relations entre l'heure solaire et l'heure de la montre
Aujourd'hui, les cadrans solaires ne rivaliseront plus jamais avec nos montres à quartz. On en construira un par nostalgie des temps anciens, pour la beauté de l'appareil, et aussi peut-être pour le plaisir de comprendre un petit bout de la mécanique céleste. Donc essayons de le faire le plus juste possible.
On aborde une partie ardue qui fait intervenir la latitude, la longitude, le méridien de référence (heure d'été, heure d'hiver), la déclinaison terrestre, l'équation du temps ... Les gnomonistes ont l'habitude d'utiliser les lettres grecques phi (φ), lambda (λ) et delta (δ), pour respectivement, la latitude, la longitude et la déclinaison de la terre.
Heure d'hiver, heure d'été, Méridien de référence, Correction n° 1
Wikipédia nous donne les longitudes de Strasbourg : λ = 7° 45' 08" (Est), et de Brest : λ = 4° 29' 08" (Ouest). Traduites en décimal cela fait, -7,7522° pour Strasbourg et +4,4856° pour Brest. L'écart de longitude est : 4,4856 - (-7,7522) = 12,2378°. Sachant que le soleil parcourt 360° en 24 heures, c'est à dire 15° par heure, lorsqu'il est sur Strasbourg, pour arriver à Brest il faudra attendre : 12,2378/15 = 0,8159 = 48 minutes et 57 secondes.
A l'intérieur d'un pays, pour être sûr de prendre le train à l'heure, on doit tous avoir la même heure, celle d'un méridien pris comme référence. Pour le monde, la référence est Greenwich (ou presque). On peut ainsi calculer l'heure solaire (par rapport à Greenwich), lorsque,
- Le soleil est sur Strasbourg : 12 + (-7,7522) /15 = 12 - 0,5168 = 11,4832 = 11 h 28 mn et 59 s.
- Le soleil est sur Brest : 12 + 4,4856/15 = 12 + 2,1368/15 = 12,2990 = 12 h 17 mn et 57 s.
Pour la France, le méridien de référence est 15° à l'Est de Greenwich, pour l'heure d'hiver (- 15°) et 30° à l'Est de Greenwich pour l'heure d'été (- 30°).
Application pratique, pour un cadran solaire à Le Catelet (02)
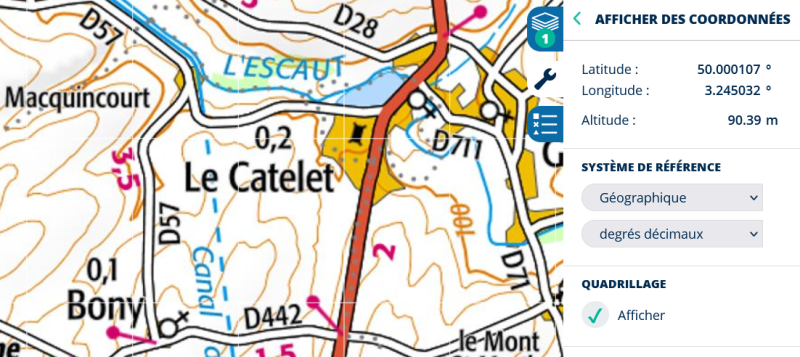
- Je vais sur GéoPortail (https://www.geoportail.gouv.fr/), je demande à afficher les coordonnées, je pointe Le Catelet dans l'Aisne. Il me dit : λ = -3,245° (avec le signe moins pour la longitude Est). On se servira plus tard de la latitude φ = 50,000°
- L'écart entre Le Catelet et le méridien de référence pour l'heure d'hiver est : -3,245 - (-15) = 11,755°
- 11,755/15 = 0,7837 = 47 mn et 1 seconde. Il faudra ajouter 47 mn et 1 s à l'heure solaire de Le Catelet pour trouver l'heure de la montre.
- L'été, il faudra ajouter 1 h 47 mn et 1 seconde.
Correction n° 2, Equation du temps
Il faut savoir que le jour solaire n'est pas exactement de 24 heures tous les jours de l'année. Ce n'est pas un caprice. C'est au contraire le résulat de la mécanique céleste rigoureuse. Les deux causes principales de la variation de la durée du jour sont : la déclinaison terrestre et l'orbite légèrement elliptique de la rotation de la terre autour du soleil. La valeur de la correction globale s'appelle Equation du temps.
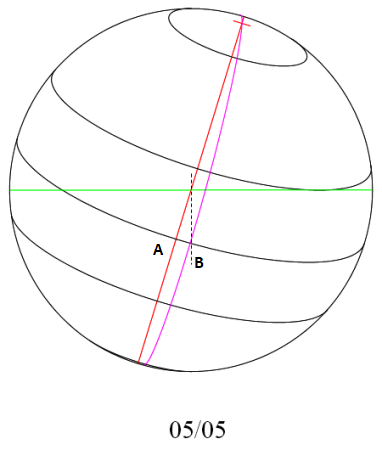

Réduction à l'équateur
La ligne verte représente le plan écliptique, ou presque, plan dans lequel évolue la terre pendant une année. Aux différentes dates, le soleil voit l'inclinaison de la terre (sa déclinaison), de différentes manières. La réduction à l'équateur est la différence entre les points A et B. Cette différence est importante le 5 mai. Elle s'annule aux équinoxes et solstices, puis elle change de sens ...
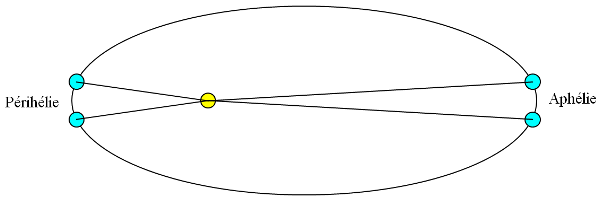
Equation au centre
Il s'agit simplement de la vitesse de la terre sur son orbite, qui s'accélère au périhélie.
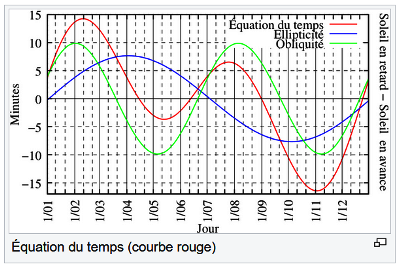
Aperçu des variations de l'équation du temps
Ces courbes prises sur Wikipédia montrent bien les deux composantes (ellipticité et obliquité) de l'équation du temps. De plus, la légende en ordonnées à droite précise clairement : "Soleil en retard" ou "Soleil en avance". Il faut en effet faire très attention dans l'utilisation des tables à propos du signe de E (valeur de l'équation du temps). On trouve dans la littérature les deux cas de figures opposés.
Conclusion, relation globale entre Hs et Hm
| Avec | λ0 | La longitude du méridien de référence (-15° l'hiver et -30° l'été) | ||
| λ | La longitude du lieu d'observation exprimée en degrés | |||
| E | La valeur de l'équation du temps le jour de l'observation exprimée en minutes décimales | |||
| Hs | L'heure solaire exprimée sous forme décimale | |||
| Hm | L'heure légale (heure de la montre) exprimée sous forme décimale | |||
| Relation | Hm = Hs + (λ - λ0)/15 + E/60 |
Tables de la déclinaison terrestre (δ) et de l'équation du temps (E)
Les valeurs sont déterminées suivant le formulaire de Denis Savoie, La Gnomonique, Les Belles Lettres, méthode n° 1, page 53. Ce sont les moyennes des quatre années 2021 à 2024.
| Date | δ en degrés | E en mn | Date | δ en degrés | E en mn | Date | δ en degrés | E en mn | Date | δ en degrés | E en mn | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/1 | -22,99 | 3,50 | 1/4 | 4,59 | 3,91 | 1/7 | 23,10 | 3,87 | 1/10 | -3,24 | -10,30 | |||
| 2/1 | -22,90 | 3,97 | 2/4 | 4,98 | 3,62 | 2/7 | 23,03 | 4,06 | 2/10 | -3,63 | -10,62 | |||
| 3/1 | -22,81 | 4,44 | 3/4 | 5,36 | 3,32 | 3/7 | 22,95 | 4,24 | 3/10 | -4,01 | -10,94 | |||
| 4/1 | -22,71 | 4,89 | 4/4 | 5,74 | 3,03 | 4/7 | 22,86 | 4,42 | 4/10 | -4,40 | -11,25 | |||
| 5/1 | -22,60 | 5,34 | 5/4 | 6,12 | 2,74 | 5/7 | 22,77 | 4,60 | 5/10 | -4,78 | -11,55 | |||
| 6/1 | -22,48 | 5,78 | 6/4 | 6,50 | 2,46 | 6/7 | 22,67 | 4,77 | 6/10 | -5,17 | -11,85 | |||
| 7/1 | -22,35 | 6,22 | 7/4 | 6,88 | 2,18 | 7/7 | 22,57 | 4,93 | 7/10 | -5,55 | -12,14 | |||
| 8/1 | -22,22 | 6,65 | 8/4 | 7,25 | 1,90 | 8/7 | 22,46 | 5,09 | 8/10 | -5,93 | -12,43 | |||
| 9/1 | -22,08 | 7,06 | 9/4 | 7,63 | 1,62 | 9/7 | 22,34 | 5,24 | 9/10 | -6,31 | -12,70 | |||
| 10/1 | -21,94 | 7,47 | 10/4 | 8,00 | 1,35 | 10/7 | 22,22 | 5,38 | 10/10 | -6,69 | -12,97 | |||
| 11/1 | -21,78 | 7,87 | 11/4 | 8,37 | 1,09 | 11/7 | 22,08 | 5,52 | 11/10 | -7,07 | -13,23 | |||
| 12/1 | -21,62 | 8,26 | 12/4 | 8,73 | 0,83 | 12/7 | 21,95 | 5,65 | 12/10 | -7,45 | -13,49 | |||
| 13/1 | -21,45 | 8,64 | 13/4 | 9,10 | 0,57 | 13/7 | 21,80 | 5,77 | 13/10 | -7,82 | -13,73 | |||
| 14/1 | -21,28 | 9,01 | 14/4 | 9,46 | 0,32 | 14/7 | 21,66 | 5,89 | 14/10 | -8,19 | -13,97 | |||
| 15/1 | -21,10 | 9,36 | 15/4 | 9,82 | 0,08 | 15/7 | 21,50 | 5,99 | 15/10 | -8,56 | -14,20 | |||
| 16/1 | -20,91 | 9,71 | 16/4 | 10,17 | -0,16 | 16/7 | 21,34 | 6,09 | 16/10 | -8,93 | -14,42 | |||
| 17/1 | -20,72 | 10,05 | 17/4 | 10,52 | -0,39 | 17/7 | 21,17 | 6,18 | 17/10 | -9,30 | -14,63 | |||
| 18/1 | -20,51 | 10,37 | 18/4 | 10,87 | -0,62 | 18/7 | 21,00 | 6,26 | 18/10 | -9,66 | -14,82 | |||
| 19/1 | -20,31 | 10,68 | 19/4 | 11,22 | -0,84 | 19/7 | 20,82 | 6,33 | 19/10 | -10,02 | -15,01 | |||
| 20/1 | -20,09 | 10,98 | 20/4 | 11,57 | -1,05 | 20/7 | 20,63 | 6,39 | 20/10 | -10,38 | -15,19 | |||
| 21/1 | -19,87 | 11,26 | 21/4 | 11,91 | -1,26 | 21/7 | 20,44 | 6,44 | 21/10 | -10,74 | -15,36 | |||
| 22/1 | -19,65 | 11,54 | 22/4 | 12,24 | -1,45 | 22/7 | 20,24 | 6,48 | 22/10 | -11,10 | -15,51 | |||
| 23/1 | -19,41 | 11,80 | 23/4 | 12,58 | -1,64 | 23/7 | 20,04 | 6,51 | 23/10 | -11,45 | -15,66 | |||
| 24/1 | -19,17 | 12,05 | 24/4 | 12,91 | -1,83 | 24/7 | 19,83 | 6,54 | 24/10 | -11,80 | -15,79 | |||
| 25/1 | -18,93 | 12,28 | 25/4 | 13,24 | -2,00 | 25/7 | 19,62 | 6,55 | 25/10 | -12,14 | -15,91 | |||
| 26/1 | -18,68 | 12,50 | 26/4 | 13,56 | -2,17 | 26/7 | 19,40 | 6,55 | 26/10 | -12,48 | -16,02 | |||
| 27/1 | -18,42 | 12,71 | 27/4 | 13,88 | -2,33 | 27/7 | 19,18 | 6,55 | 27/10 | -12,82 | -16,12 | |||
| 28/1 | -18,16 | 12,91 | 28/4 | 14,20 | -2,48 | 28/7 | 18,95 | 6,53 | 28/10 | -13,16 | -16,21 | |||
| 29/1 | -17,89 | 13,09 | 29/4 | 14,51 | -2,62 | 29/7 | 18,71 | 6,50 | 29/10 | -13,49 | -16,28 | |||
| 30/1 | -17,62 | 13,25 | 30/4 | 14,82 | -2,75 | 30/7 | 18,47 | 6,47 | 30/10 | -13,82 | -16,34 | |||
| 31/1 | -17,34 | 13,41 | 1/5 | 15,12 | -2,88 | 31/7 | 18,23 | 6,42 | 31/10 | -14,15 | -16,39 | |||
| 1/2 | -17,06 | 13,55 | 2/5 | 15,42 | -2,99 | 1/8 | 17,98 | 6,36 | 1/11 | -14,47 | -16,42 | |||
| 2/2 | -16,77 | 13,67 | 3/5 | 15,71 | -3,10 | 2/8 | 17,72 | 6,30 | 2/11 | -14,79 | -16,44 | |||
| 3/2 | -16,48 | 13,79 | 4/5 | 16,01 | -3,20 | 3/8 | 17,46 | 6,22 | 3/11 | -15,10 | -16,45 | |||
| 4/2 | -16,18 | 13,89 | 5/5 | 16,29 | -3,28 | 4/8 | 17,20 | 6,13 | 4/11 | -15,41 | -16,44 | |||
| 5/2 | -15,88 | 13,97 | 6/5 | 16,58 | -3,36 | 5/8 | 16,93 | 6,03 | 5/11 | -15,72 | -16,42 | |||
| 6/2 | -15,58 | 14,05 | 7/5 | 16,85 | -3,43 | 6/8 | 16,66 | 5,93 | 6/11 | -16,02 | -16,38 | |||
| 7/2 | -15,27 | 14,11 | 8/5 | 17,13 | -3,49 | 7/8 | 16,38 | 5,81 | 7/11 | -16,31 | -16,34 | |||
| 8/2 | -14,95 | 14,15 | 9/5 | 17,39 | -3,54 | 8/8 | 16,10 | 5,68 | 8/11 | -16,61 | -16,27 | |||
| 9/2 | -14,63 | 14,18 | 10/5 | 17,66 | -3,58 | 9/8 | 15,81 | 5,54 | 9/11 | -16,89 | -16,20 | |||
| 10/2 | -14,31 | 14,20 | 11/5 | 17,92 | -3,61 | 10/8 | 15,52 | 5,40 | 10/11 | -17,18 | -16,11 | |||
| 11/2 | -13,98 | 14,21 | 12/5 | 18,17 | -3,63 | 11/8 | 15,22 | 5,24 | 11/11 | -17,45 | -16,00 | |||
| 12/2 | -13,65 | 14,20 | 13/5 | 18,42 | -3,65 | 12/8 | 14,93 | 5,08 | 12/11 | -17,73 | -15,88 | |||
| 13/2 | -13,31 | 14,19 | 14/5 | 18,66 | -3,65 | 13/8 | 14,62 | 4,90 | 13/11 | -17,99 | -15,75 | |||
| 14/2 | -12,97 | 14,16 | 15/5 | 18,90 | -3,64 | 14/8 | 14,32 | 4,72 | 14/11 | -18,26 | -15,60 | |||
| 15/2 | -12,63 | 14,11 | 16/5 | 19,13 | -3,62 | 15/8 | 14,01 | 4,52 | 15/11 | -18,51 | -15,44 | |||
| 16/2 | -12,29 | 14,06 | 17/5 | 19,36 | -3,60 | 16/8 | 13,69 | 4,32 | 16/11 | -18,77 | -15,27 | |||
| 17/2 | -11,94 | 13,99 | 18/5 | 19,58 | -3,56 | 17/8 | 13,37 | 4,11 | 17/11 | -19,01 | -15,08 | |||
| 18/2 | -11,59 | 13,91 | 19/5 | 19,80 | -3,52 | 18/8 | 13,05 | 3,89 | 18/11 | -19,25 | -14,87 | |||
| 19/2 | -11,23 | 13,82 | 20/5 | 20,01 | -3,47 | 19/8 | 12,73 | 3,66 | 19/11 | -19,49 | -14,66 | |||
| 20/2 | -10,87 | 13,72 | 21/5 | 20,21 | -3,40 | 20/8 | 12,40 | 3,43 | 20/11 | -19,72 | -14,43 | |||
| 21/2 | -10,51 | 13,61 | 22/5 | 20,41 | -3,33 | 21/8 | 12,07 | 3,19 | 21/11 | -19,94 | -14,18 | |||
| 22/2 | -10,15 | 13,49 | 23/5 | 20,61 | -3,25 | 22/8 | 11,73 | 2,93 | 22/11 | -20,16 | -13,92 | |||
| 23/2 | -9,78 | 13,35 | 24/5 | 20,79 | -3,16 | 23/8 | 11,39 | 2,68 | 23/11 | -20,37 | -13,65 | |||
| 24/2 | -9,41 | 13,21 | 25/5 | 20,97 | -3,07 | 24/8 | 11,05 | 2,41 | 24/11 | -20,57 | -13,37 | |||
| 25/2 | -9,04 | 13,06 | 26/5 | 21,15 | -2,96 | 25/8 | 10,71 | 2,14 | 25/11 | -20,77 | -13,07 | |||
| 26/2 | -8,67 | 12,89 | 27/5 | 21,32 | -2,85 | 26/8 | 10,36 | 1,86 | 26/11 | -20,96 | -12,76 | |||
| 27/2 | -8,29 | 12,72 | 28/5 | 21,48 | -2,73 | 27/8 | 10,01 | 1,57 | 27/11 | -21,15 | -12,44 | |||
| 28/2 | -7,92 | 12,54 | 29/5 | 21,64 | -2,60 | 28/8 | 9,66 | 1,28 | 28/11 | -21,32 | -12,11 | |||
| 1/3 | -7,54 | 12,35 | 30/5 | 21,79 | -2,46 | 29/8 | 9,31 | 0,98 | 29/11 | -21,50 | -11,76 | |||
| 2/3 | -7,16 | 12,15 | 31/5 | 21,94 | -2,32 | 30/8 | 8,95 | 0,67 | 30/11 | -21,66 | -11,41 | |||
| 3/3 | -6,77 | 11,95 | 1/6 | 22,07 | -2,17 | 31/8 | 8,59 | 0,36 | 1/12 | -21,82 | -11,04 | |||
| 4/3 | -6,39 | 11,73 | 2/6 | 22,20 | -2,01 | 1/9 | 8,23 | 0,05 | 2/12 | -21,97 | -10,66 | |||
| 5/3 | -6,00 | 11,51 | 3/6 | 22,33 | -1,85 | 2/9 | 7,86 | -0,27 | 3/12 | -22,11 | -10,27 | |||
| 6/3 | -5,61 | 11,28 | 4/6 | 22,45 | -1,68 | 3/9 | 7,50 | -0,60 | 4/12 | -22,25 | -9,87 | |||
| 7/3 | -5,23 | 11,05 | 5/6 | 22,56 | -1,51 | 4/9 | 7,13 | -0,92 | 5/12 | -22,38 | -9,46 | |||
| 8/3 | -4,84 | 10,81 | 6/6 | 22,67 | -1,33 | 5/9 | 6,76 | -1,26 | 6/12 | -22,50 | -9,05 | |||
| 9/3 | -4,45 | 10,56 | 7/6 | 22,77 | -1,14 | 6/9 | 6,39 | -1,59 | 7/12 | -22,62 | -8,62 | |||
| 10/3 | -4,05 | 10,30 | 8/6 | 22,86 | -0,95 | 7/9 | 6,01 | -1,93 | 8/12 | -22,73 | -8,19 | |||
| 11/3 | -3,66 | 10,04 | 9/6 | 22,94 | -0,76 | 8/9 | 5,64 | -2,28 | 9/12 | -22,83 | -7,74 | |||
| 12/3 | -3,27 | 9,78 | 10/6 | 23,02 | -0,56 | 9/9 | 5,26 | -2,62 | 10/12 | -22,92 | -7,29 | |||
| 13/3 | -2,87 | 9,51 | 11/6 | 23,09 | -0,36 | 10/9 | 4,88 | -2,97 | 11/12 | -23,01 | -6,84 | |||
| 14/3 | -2,48 | 9,24 | 12/6 | 23,16 | -0,15 | 11/9 | 4,50 | -3,32 | 12/12 | -23,08 | -6,37 | |||
| 15/3 | -2,08 | 8,96 | 13/6 | 23,22 | 0,05 | 12/9 | 4,12 | -3,68 | 13/12 | -23,15 | -5,90 | |||
| 16/3 | -1,69 | 8,68 | 14/6 | 23,27 | 0,26 | 13/9 | 3,74 | -4,03 | 14/12 | -23,22 | -5,43 | |||
| 17/3 | -1,29 | 8,39 | 15/6 | 23,31 | 0,48 | 14/9 | 3,36 | -4,39 | 15/12 | -23,27 | -4,95 | |||
| 18/3 | -0,90 | 8,10 | 16/6 | 23,35 | 0,69 | 15/9 | 2,97 | -4,74 | 16/12 | -23,32 | -4,47 | |||
| 19/3 | -0,50 | 7,81 | 17/6 | 23,38 | 0,91 | 16/9 | 2,59 | -5,10 | 17/12 | -23,36 | -3,98 | |||
| 20/3 | -0,11 | 7,51 | 18/6 | 23,41 | 1,13 | 17/9 | 2,20 | -5,46 | 18/12 | -23,39 | -3,49 | |||
| 21/3 | 0,29 | 7,22 | 19/6 | 23,42 | 1,34 | 18/9 | 1,82 | -5,82 | 19/12 | -23,41 | -3,00 | |||
| 22/3 | 0,68 | 6,92 | 20/6 | 23,44 | 1,56 | 19/9 | 1,43 | -6,17 | 20/12 | -23,43 | -2,50 | |||
| 23/3 | 1,08 | 6,62 | 21/6 | 23,44 | 1,78 | 20/9 | 1,04 | -6,53 | 21/12 | -23,44 | -2,01 | |||
| 24/3 | 1,47 | 6,32 | 22/6 | 23,44 | 2,00 | 21/9 | 0,65 | -6,88 | 22/12 | -23,44 | -1,51 | |||
| 25/3 | 1,86 | 6,02 | 23/6 | 23,43 | 2,21 | 22/9 | 0,26 | -7,24 | 23/12 | -23,43 | -1,01 | |||
| 26/3 | 2,26 | 5,72 | 24/6 | 23,41 | 2,43 | 23/9 | -0,13 | -7,59 | 24/12 | -23,42 | -0,51 | |||
| 27/3 | 2,65 | 5,41 | 25/6 | 23,38 | 2,64 | 24/9 | -0,52 | -7,94 | 25/12 | -23,39 | -0,02 | |||
| 28/3 | 3,04 | 5,11 | 26/6 | 23,35 | 2,85 | 25/9 | -0,90 | -8,29 | 26/12 | -23,36 | 0,48 | |||
| 29/3 | 3,43 | 4,81 | 27/6 | 23,32 | 3,06 | 26/9 | -1,29 | -8,63 | 27/12 | -23,32 | 0,97 | |||
| 30/3 | 3,82 | 4,51 | 28/6 | 23,27 | 3,27 | 27/9 | -1,68 | -8,97 | 28/12 | -23,28 | 1,46 | |||
| 31/3 | 4,21 | 4,21 | 29/6 | 23,22 | 3,47 | 28/9 | -2,07 | -9,31 | 29/12 | -23,22 | 1,95 | |||
| 30/6 | 23,16 | 3,67 | 29/9 | -2,46 | -9,65 | 30/12 | -23,16 | 2,43 | ||||||
| 30/9 | -2,85 | -9,98 | 31/12 | -23,09 | 2,91 | |||||||||
Construire un cadran solaire
Le but est d'arriver à dessiner un cadran pour un mur vertical déclinant. C'est un exercice de géométrie dans l'espace. On va localiser le cadran équatorial, lequel nous servira de base pour dessiner le cadran vertical déclinant. Tout d'abord on va repérer qu'il existe sur terre un cadran horizontal dont le plan est parallèle à celui du mur sur lequel on veut travailler. Leur dessin sera identique.
Translation de cadrans
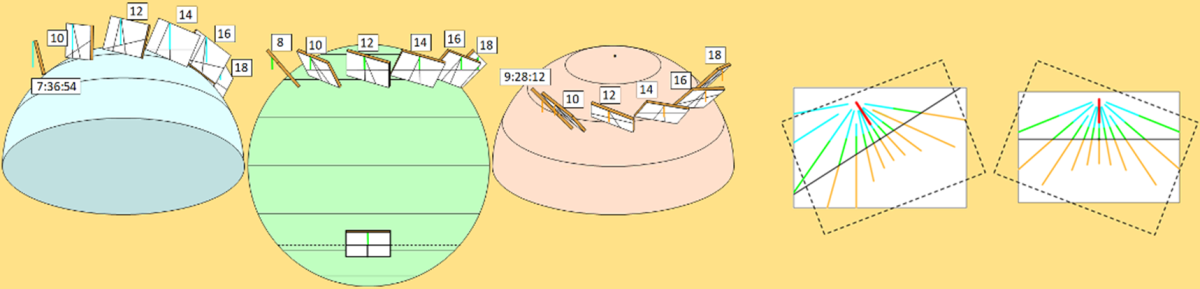
Au chapitre "Les cadrans solaires, dernière section "Les cadrans horizontaux et verticaux, et dernière sous-section "Dessin des différents cadrans", la ressemblance a été évoquée entre le dessin du vertical et celui du vertical déclinant. En fait maintenant on va comparer les deux cadrans suivants qui sont représentés sur ce dessin :
- Le vertical tracé pour le parallèle de 45° et dont la table est parfaitement au soleil à 14 heures solaires (longitude -30°). C'est un cadran occidental.
- L'horizontal tracé pour le parallèle de latitude = -40,89° (dans l'hémisphère sud), à la longitude 0°.
Les dessins de ces deux cadrans sont parfaitement superposables après une rotation de 20,71°, car leur table est parallèle l'une à l'autre. Qu'on se rassure il n'est pas question de calculer les caractéristiques de ce cadran horizontal. Il faut simplement retenir que ce cadran horizontal a un axe de symétrie vertical. Le but est de retrouver cet axe de symétrie sur le vertical déclinant. Par ailleurs, il y a une ligne très importante : la ligne noire horizontale du cadran horizontal. C'est la ligne par laquelle passe le cadran équatorial qui va nous servir de base. Cette ligne a bien sûr pivoté sur le vertical déclinant. Il faudra qu'on la retrouve.
A partir de maintenant, on se retrousse les manches.
Préparatifs
Ombre d'un point

On aura besoin de tracer la progression de l'ombre d'un point au cours d'une journée. Quel doit être ce point ?
Le soleil a un diamètre de 1,4 millions de km. Il est à une distance de 150 millions de km. Il nous apparait sous un angle de un demi degré. Un petit point opaque ne donne pas d'ombre. Une bille de 3,7 mm de diamètre ne donne pas d'ombre à 40 cm de distance. Pour avoir une ombre visible il ne faudrait pas dépasser 20 cm de distance. Sachant que dès qu'on s'éloigne du point H projection orthogonale, la distance de la bille à la table s'allonge, si on choisit de positionner la bille à 20 cm de la table, il faut que la bille ait un diamètre d'au moins 5 mm. On peut aussi utliser un œilleton. Le raisonnement est le même pour la taille du trou.
Matériel
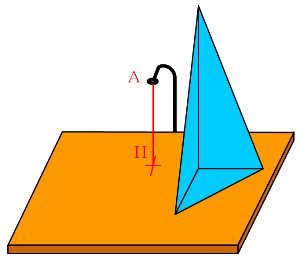
- Une planche, du papier, du scotch, de quoi écrire, règle, compas, niveau, fil à plomb, équerre volumique, dispositif de suivi du soleil.
- Utiliser une planche de dimension 40x30 cm au moins, par exemple une étagère neuve, (non voilée par une charge subie dans le passé). On vérifie sa planéïté par un examen de profil, en recherchant les "jours" éventuels (passage de lumière) contre une règle posée dans différentes directions.
- Le mur lui-même n'est peut-être pas forcément rigoureusement plan. On doit faire la mesure à l'endroit précis où on veut poser le cadran.
- Vérifier la verticalité du mur. Si ce n'est le cas, il y a deux solutions :
- Ramener à la verticalité avec des cales qui devront être reproduites pour le cadran définitif.
- Mesurer l'inclinaison effective qu'on tentera d'assimiler à une modification de la latitude.
- Fixer le dispositif de suivi (la bille, l'œilleton). Choisir au début une distance de 10 cm au-dessus de la planche, à peu près au centre en largeur et plutôt dans le haut. Les ombres sur les cadrans verticaux sont longues l'été. On aura surement besoin de tatonner pour la position de ce point source d'ombre.
- Repérer le point H, projection orthogonale de A, la bille, à l'aide de l'équerre "volumique" ou à défaut en déplaçant une équerre plate dans plusieurs directions. Bien sûr il s'agit de la projection du centre de la bille.
- Tracer plusieurs cercles de centre H. Par exemple 10, 15, 20, 25 cm de rayon.
- Fixer sommairement la planche au mur, mais de manière suffisamment rigide pour qu'elle ne bouge pas pendant les mesures.
- Tracer la verticale passant par H, ainsi que l'horizontale. Ces lignes seront les axes de repérage des coordonnées des points.
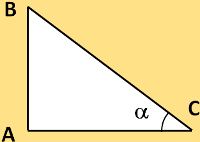
Rappel de quelques rudiments de trigonométrie
Ce sont des rapports de longueur des côtés du triangle rectangle en relation avec l'angle.
| Le sinus de l'angle | sin α = AB/BC |
| Le cosinus de l'angle | cos α = AC/BC |
| La tangente de l'angle | tg α = AB/AC |
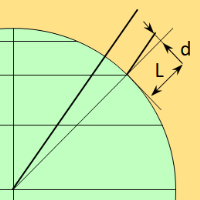
Verticalité du mur
On mesure simplement la déviation d du mur en millimètres par rapport à une règle verticale de longueur L. L'angle recherché a une tangente dont la valeur est d/L. Par exemple, si ma règle a une longueur L = 1000 mm et que j'observe une déviation de 12 mm, je fais 12/1000 = 0,012 et avec la touche Arc Tg (ou bien tg-1), j'obtiens 0,69°. A condition que cette inclnaison ne soit pas trop importante on peut l'assimiler à un déplacement du cadran vers une latitude φ augmentée de 0,69°.
Recherche de la sous-stylaire
La sous-stylaire est le fameux axe de symétrie qui représente le plan du midi du cadran, le moment où le cadran est exactement face au soleil. Pour la trouver nous devons tracer un arc diurne, trajectoire de l'ombre d'un point un jour donné. Notre matériel est prêt.
Méthode des cercles indiens
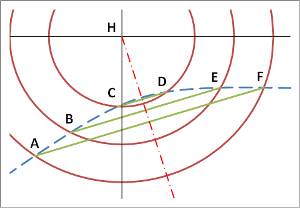
Nos cercles sont tracés. Par un jour ensoleillé, de temps en temps, et si possible au passage des cercles, on fait une croix sur la position de l'ombre et on note l'heure. La mesure est faite à Le Catelet (φ = 50,000°, λ = -3,245°), le 8 août (δ = 16,10°, E = 5,68 mn). Voici les relevés effectués et les calculs correspondants :
| Point | A | B | C | D | E | F | Segment | F - A | E - B | D - C | Moyenne | |
| Heure de la montre | 12:17 | 12:56 | 14:32 | 16:53 | 18:29 | 19:08 | (Hm1 + Hm2)/2 | 15:43 | 15:43 | 15,43 | 15:43 | |
| Heure solaire | 10:25 | 11:03 | 12:40 | 15:00 | 16:37 | 17:15 | (Hs1 + Hs2)/2 | 13:50 | 13:50 | 13:50 | 13:50 | |
| x | -155 | -91 | -8 | 80 | 176 | 253 | x2 - x1 | 408 | 267 | 88 | ||
| y | -221 | -178 | -130 | -103 | -95 | -95 | y2 - y1 | 126 | 83 | 27 | ||
| Pente (y2 - y1)/(x2 - x1) | 0,3088 | 0,3109 | 0,3068 | 0,3088 | ||||||||
| Angle e en degrés | 17,161 | 17,269 | 17,057 | 17,162 | ||||||||
La pente calculée est celle des lignes AF, BE et CD. L'angle e est l'angle de ces droites avec l'axe des x. L'axe de symétrie recherché est perpendiculaire. L'angle avec l'axe des y vaut également e. Nous avons la pente de notre sous-stylaire.
Les heures moyennes de celles des extrémités de chaque segment, sont évidemment faites en passant par la forme décimale. C'est l'heure à laquelle
le cadran est exactement face au soleil. On pourra affiner cette valeur le jour suivant, après avoir tracé la médiatrice commune.
Rappel : Hm = Hs + (λ - λ0)/15 + E/60 = Hs + (-3,245 + 30)/15 + 5,68/60 = Hs + 1,8783 (ce jour là et à cette longitude).
Il y a une relation qui permet de vérifier la cohérence entre l'angle e et l'heure du midi du cadran.
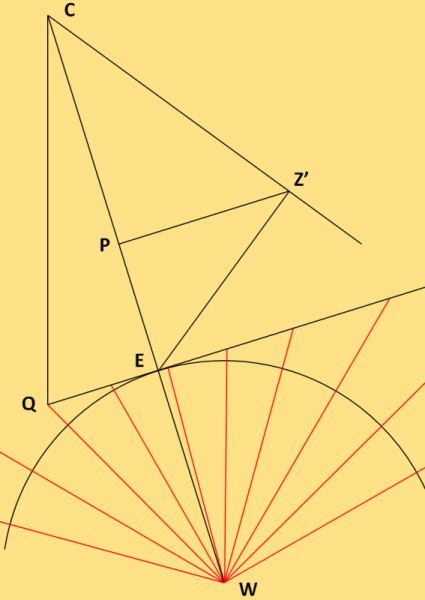
| Le décalage entre l'heure du midi du cadran et le midi local est : 13:50 - 12 = 1:50 | ||
| On transforme ce décalage en angle horaire (l'angle QWE) : 1:50 = 1,8333 | ||
| A raison de 15° par heure, on calcule l'angle c = QWE | c = 15 x 1,8333 = 27,5° | |
| On calcule l'angle f de Michel Lalos, angle WCZ' | tg f = cos c/tg φ | |
| tg f = cos(27,5)/tg(50) = 0,8870/1,1918 | tg f = 0,7443 | |
| Sur la calculette on fait tg-1 ou Arc tg | Le résultat est : f = 36,6600° | |
| On devrait maintenant retrouver la valeur de e, en faisant | ||
| cos e = sin φ /cos f | cos e = sin(50)/cos(36,660) | |
| Le résultat est : e = 17,266 | Comparé à 17,162 | |
| Un dixième de degré d'erreur. | ||
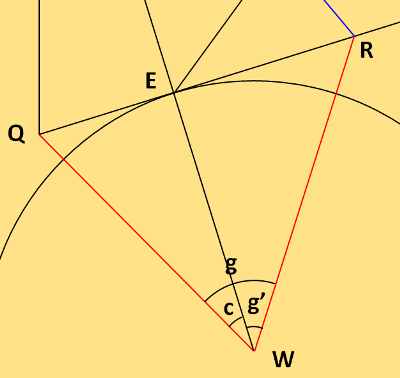
Tracé du cadran
Comme promis au début, nous allons positionner quelques points, puis tracer les lignes horaires par construction géométrique. Les noms des repères sont ceux de Michel Lalos, avec en plus ceux qu'il n'a pas nommés, les points E et Z'.
La dimension de référence est j, celle du segment QC qui a été choisi.
Les coordonnées des points sont données par rapport à Q, pris comme origine. On dira par exemple xC pour l'abscisse du point C et yC pour son ordonnée.
Toutes les dimensions sont calculées en fonction de j et des trois angles c, e et f.
Rappel e = QCW est l'inclinaison de la sous-stylaire et f = WCZ' est en rapport avec la position de l'aiguille.
L'aiguille dans l'espace réel
Le plan méridien du cadran a été rabattu pour faciliter le tracé. Dans la réalité, il faut plier autour de EC pour ramener ce plan dans sa position orthogonale à la table. L'aiguille est CZ'. Elle est plantée en C sur la table, sur le cadran. Pour faciliter son positionnement, quelques dimensions sont données plus loin.
Position des points
| Abscisse | Ordonnée | Avec j = 100 ; e = 17,266 et f = 36,660 | |||
| Racine de l'aiguille | C | xC = 0 | yC = j/cos e | xC =0 | yC = 104,72 |
| Midi du cadran sur la ligne équatoriale | E | xE = j sin e | yE = j sin e tg e | xE = 29,68 | yE = 9,23 |
| Racine des lignes horaires équatoriales | W | xW = j sin e(1 + sin f) | yW = j(sin e tg e - sin f cos e) | xW = 47,40 | yW = -47,79 |
| Midi local sur la ligne équatoriale | Q | xQ = 0 | yQ = 0 | xQ = 0 | yQ = 0 |
| Projection de l'extrémité de l'aiguille Z' sur la table | P | xP = HP = j sin e cos2 f | yP = j(1/cos e - cos2 f cos e) | xP = 19,10 | yP = 43,27 |
| Distance de l'extrémité de l'aiguille à la table | PZ' = j sin f cos f corrigé en PZ' = j (signe de e) sin f cos f | PZ' = 47,90 | |||
| Extrémité de l'aiguille | Z' | xZ' = HP + PZ' cos e | yZ' = yP + PZ' sin e | xZ' = 64,84 | yZ' = 57,49 |
| Point équatorial à 18 heures solaires | T | xT = yP/tg e | yT = yP | xT = 139,21 | yT = 43,27 |
Position de l'aiguille
| Segment | CZ' | PZ' | EZ' | CP | PE | QZ' (réél) |
| Formule | j cos f | j sin f cos f | j sinf | j cos2 f | j sin2 f | j sin f/cos c |
| Résultat avec j = 100 ; c = 27,5 ; e = 17,266 ; f = 36,660 | 80,22 | 47,90 | 59,71 | 64,35 | 35,65 | 67,31 |
Tracé des heures
Comme pour le plan méridien, pour faciliter le tracé, le plan équatorial est rabattu. En réalité il faut plier autour de la ligne QE (QT) jusqu'à ramener W sur le point Z'. A remarquer que le plan équatorial est réellement en Z' (non en Z), car l'aiguille est orthogonanale à ce plan. Il faut que EZ'C soit droit. En prenant Z au lieu de Z' cela ne change pas la justesse du cadran, cela change juste la longueur de l'aiguille et donc la longueur de l'ombre. L'utilisation de Z' permet de justifier le nom d'équinoxiale donné à QT. En effet aux équinoxes de printemps et d'automne, δ vaut 0°, la terre est droite, le soleil est pile face à l'équateur. Cela se traduit sur le cadran à des ombres de l'aiguille qui partent de C et s'arrêtent sur cette ligne équatoriale, l'équinoxiale, à condition que l'aiguille ait bien la longueur CZ'.
Pour tracer les heures on commence par le cadran équatorial en WQT. Le midi solaire est sur WQ. On place donc notre rapporteur, centré sur W et avec le zéro sur la ligne WQ. La ligne WT est sur 90°. On marque tous les angles de 15 en 15°. On trace les segments de chaque angle en partant de W et on poursuit jusqu'à la ligne QT.
On s'occupe ensuite des lignes horaires du vrai cadran. Il sufit de tracer les segments qui partent du point C jusqu'à chacun des croisements des heures équatoriales avec le ligne QT. Sur le croquis seul le cadran équatorial a été tracé. Pour voir le tracé complet, il faut remonter au croquis initial qui est le symétrique de celui-ci. Celui-ci est un cadran occidentental (tourné vers l'ouest), celui-là est un cadran oriental (tourné vers l'est). Les angles caractéristiques du cadran du début sont : φ = 50°, λ = -3,245°, le 8 août (δ = 16,10°, E = 5,68 mn), c = -27,5°, e = -17,266°, f = 36,66°.
Utilisation des angles négatifs
Il faut savoir que : sin 30 = 0,5 ; sin -30 = -0,5 ; tg 45 = 1; tg -45 = -1 ; mais, cos 60 = 0,5 et cos -60 = 0,5. En trigonométrie il faut
toujours avoir un œil critique, car par exemple avec l'utilisation des cosinus on peut perdre un signe moins.
Lorsqu'on trace un cadran oriental, la ligne CQ est à droite et il y a beaucoup d'abscisses qui sont négatives. Est-ce bien le cas ?
Pour le triangle oriental l'angle f reste positif (dans l'hémisphère Nord), seuls c et e sont négatifs.
En fait le plus simple est de refaire tous les calculs avec les nouveaux signes. On devrait trouver toutes les ordonnées identiques et les
abscisses opposées.
Il y a un souci avec Z'. Pour rétablir les bonnes valeurs on doit orienter le segment PZ', en lui donnant le signe de e.
Tracé des heures (bis)
Si on n'est pas trop rebuté par la trigo, il y a une autre façon de faire.
Pour représenter une heure h par le segment WR puis CR, on peut calculer la distance ER.
Midi étant sur WQ, il faut d'abord déterminer la valeur de l'angle g = QWR. On fait d'abord h - 12 puis on multiplie par 15 pour avoir en
degrés d'angle.
Par exemple pour h = 16 heures : g = 15(16 - 12) = 60°. Mais si je veux utiliser la tangente de EWR, je dois travailler avec g' = EWR.
Par chance je connais c qui est le décalage angulaire entre le midi du cadran (en WE) et le midi local (en WQ). g' = g - c
Et ER = WE tg g'. Avec WE = EZ' = j sin f, en définitive on a : ER = j sin f tg[15(h - 12) - c]
| Heure h | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| g | -30 | -15 | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 |
| g' | -57,5 | -42,5 | -27,5 | -12,5 | 2,5 | 17,5 | 32,5 | 47,5 | 62,5 | 77,5 |
| ER | -93,7 | -54,7 | -31,1 | -13,2 | 2,6 | 18,8 | 38,0 | 65,2 | 114,7 | 269,3 |
Il ne reste plus qu'à pointer et tirer les traits.
Les maximes
Beaucoup de maximes se rapportent à la mort, la fuite inexorable sans retour, mais il y a aussi les bons vivants et l’amour et, l’insouciance de la jeunesse, la religion et la nécessité de la présence du soleil. Voici un échantillon suivant le classement de Pierre Ricou et Jean-Marie Homet "Cadrans du soleil", éditions Jeanne Laffitte :
| La Mort | O voyageur voici l'heure, Pense à ta dernière demeure | St Siméon de Bressieux | 38 |
| Ici tu verras l'heure, Et plus bas ta demeure | Saint Savin | 38 | |
| sur | Les temps sont comptés | Roybon | 38 |
| 40 % | Nous ne savons ni le jour ni l'heure | Paladru | 38 |
| des | La mort n'a point d'heure fixe | Eybens | 38 |
| cadrans | Vivre n'est pas autre chose que mourir | Les Avenières | 38 |
| Redoute la dernière | Claix | 38 | |
| Une suffit | Arandon | 38 | |
| La dernière est cachée | Névache | 05 | |
| Tu vois l'heure, tu ignores la tienne | La Colle | 06 | |
| Prends garde à l'une d'elles | Val, près de Brignolles | 83 | |
| Le temps fuit et la mort le suit | Le Périer | 38 | |
| L'heure approche | Saint Marcellin | 38 | |
| L'ombre reviendra, l'homme jamais | La Rivière | 38 | |
| La vie passe comme les fleurs | Moirans | 38 | |
| Le temps passe et toi aussi | Virieu | 38 | |
| Toutes les heures nous blessent, la dernière nous tue | Le Villar Saint Pancrace | 05 | |
| Le Fontenil sous Briançon | 05 | ||
| Maison Claire | 05 | ||
| La Salle | 05 | ||
| La Cluze | 05 | ||
| Névache | 05 | ||
| Les Avenières | 38 | ||
| Elle fuit hélas | Plamplinet | 05 | |
| Elles blessent toutes, c'est la dernière qui tue | Ossès | 64 | |
| ... | |||
| La Vie | C’est l’heure de bien vivre | Apprieu | 38 |
| C'est l'heure de boire | Beaucroissant | 38 | |
| sur | A la bonne heure | Villeneuve | 04 |
| 25 % | Autant boire ici qu'ailleurs | Saint Didier de la Tour | 38 |
| des | Ne les compte pas, mets les à profit | Saint Hilaire du Rosier | 38 |
| cadrans | Qu'elle soit aimable celle que tu désires | Saint Chaffrey | 05 |
| Que l'heure présente vous soit favorable | Briançon | 05 | |
| Voici l'heure d'être heureux | Peymeinade | 06 | |
| ... | |||
| Le Soleil | Le soleil se lève pour toi | Cervières | 05 |
| Pas de soleil, pas d’ombre | Malaucène | 84 | |
| sur | Sans le soleil je suis silencieux | Cervières | 05 |
| 15 % | Val des Prés | 05 | |
| des | Le Villard | 05 | |
| cadrans | Si le soleil se tait, je me tais | Sospel | 06 |
| L'ombre obéit au soleil | Sénanque | 84 | |
| Œuvre du soleil et de l'ombre | Grasse | 06 | |
| Où l'ombre tombe je marque l'heure | Bétenoud | 05 | |
| Bon jour, bon soir | Saint Hilaire | 38 | |
| Saint Quentin | 38 | ||
| ... | |||
| Le reste | Sans le soleil je ne suis rien et toi sans Dieu tu ne peux rien | Claix | 38 |
| Il est plus tard que jeunesse ne pense | Pelvoux | 05 | |
| sur | Gloire à Dieu qui peut tout | Sillans | 83 |
| 20 % | Le Christ est avec nous | Larche | 04 |
| des | Le jour chasse le jour | Izeaux | 38 |
| cadrans | Le temps court sans jamais s'arrêter | Izeaux | 38 |
| Le printemsp ne dure pas toujours | Hameau des Glaises | 38 | |
| Tu les comptes, elles fuient | Virieu | 38 | |
| Nos jours passent comme l'ombre | Grasse | 04 | |
| Une de plus une de moins | Annecy | 74 | |
| Il est plus tard que vous ne croyez | Abriès | 05 | |
| Elle fuit, hélas | Plampinet | 05 | |
| N'en perds aucune | Fontienne | 04 | |
| Après le travail le repos | Le Bez | 05 | |
| C'est l'heure de faire le bien | Beauvallon | 83 | |
| N’importe quelle heure pour les amis | St Nicolas xde Macherin | 38 | |
| A qui sait aimer, les heures sont roses | Le Bez | 05 | |
| Dieu fait toujours de la géométrie | Viroflay | 78 |
Dernières précisions
Quelques détails avant de nous quitter
Les images de la page "Accueil"
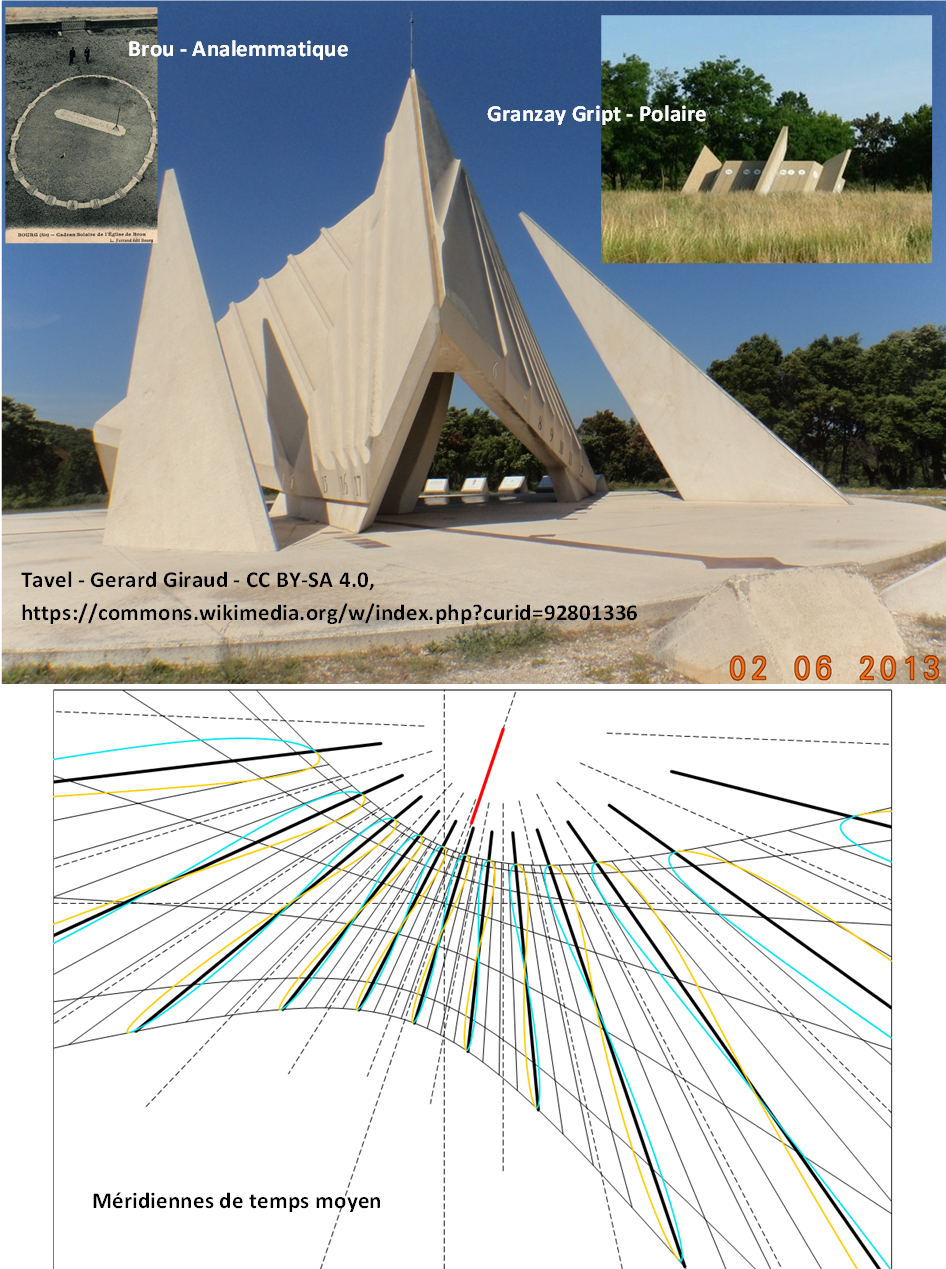
Tavel
C'est un gros monument qu'on peut voir sur une aire d'autoroute, près de Nîmes. Il y a de nombreuses faces qui se relayent suivant l'heure. La documentation trouvée sur place est très riche.
Granzay Gript
Dans les Deux-Sèvres près de Niort, près d'une aire d'autoroute (encore), on trouve ce cadran polaire. Un regret : aucune information trouvée sur place. Après avoir écrit à la mairie, la réponse a été : "Nous avons de la documentation à la mairie.
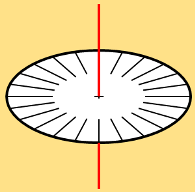
Brou
A Bourg en Bresse, dans la cour d'un monastère, on trouve ce cadran analemmatique. C'est un cadran horizontal avec un "bâton" vertical comme le gnomon des anciens. Grâce à François Vauzelard qui a su trouver une formule de calcul simple, on peut obtenir une réponse juste de l'appareil en déplaçant le bâton sur différents repères en fonction de la date.
Le résultat est que, à une heure donnée, les ombres changent de direction en fonction de la date, mais, elles passent toujours par le même point. Ainsi on on a un point pour midi, un autre point de croisement pour 13 heures ...
Méridiennes de temps moyen
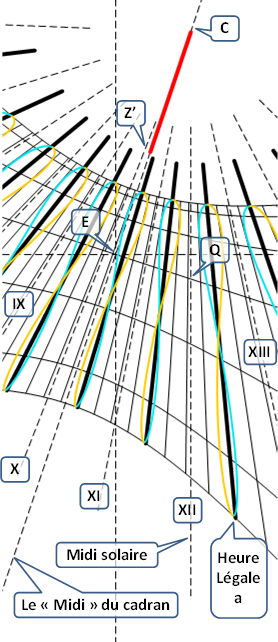
Le dessin de ce cadran est touffu. Il a juste l'avantage de remettre une couche sur les relations entre l'heure solaire et l'heure de la montre.
Le trait rouge représente la projection de la position de l'aiguille qui est plantée en C. Son extrémité arrive en Z' en avant du cadran.
Il faut ensuite s'intéresser aux traits en tirets. On a d'abors les deux axes, horizontaux et verticaux avec leur origine en E, le fameux point où l'ombre de l'aiguille a son extrémité aux équinoxes et au midi du cadran. Les autres lignes en tirets, qui concourent en C, sont les traces des ombres à chacune des heures solaires. Ces heures solaires sont notées en chiffres romains, en remarquant bien que le midi solaire local est toujours vertical.
On regarde ensuite les traits noirs continus, en commençant par les gras. A notre longitude de -6° aux alentours de Grenoble, on a déjà vu que : Hm = Hs + (λ - λ0)/15) + ... L'heure de la montre l'hiver est donc Hm = Hs + (-6 - (-15)/15 = Hs + 9/15 = Hs + 0,6 = Hs + 36 mn. Le midi de la montre est 36 mn avant le midi solaire. Donc l'heure a du dessin est celle de 13 h l'hiver et 14 h l'été. On trouve sur le dessin un trait fin tous les quarts d'heure. C'est une heure "moyenne" (juste la correction n° 1), car on n'a pas tenu compte de l'équation du temps. Il y a aussi des traits (courbes) continus fins noirs qui sont les arcs diurnes, trajectoire de l'extrémité de l'ombre au cours d'une journée. Du bas vers le haut, les dates de chacun des arcs diurnes sont : 21 juin (δ = 23,44°) : 20 mai ou 23 juillet (δ = 20°) ; 16 avril ou 27 août (δ = 10°) ; 21 mars ou 23 septembre (δ = 0°) ; 22 février ou 19 octobre (δ = -10°) ; 20 janvier ou 21 novembre (δ = 20°) ; 22 décembre (δ = -23,44°).
Pour tenir compte de l'équation du temps il faut profiter du fait que la longueur de l'ombre change en fonction de la date. On se sert maintenant des courbes en couleurs. Du 21 décembre au 21 juin il faut regarder les courbes bleues, et du 21 juin au 21 décembre, on regarde les courbes jaunes. On voit que la correction supplémentaire due à l'équation du temps est environ de plus ou moins un quart d'heure.
Val des Prés (05)
Un des cadrans solaires de la vallée de la Clarée, Névache.
Déclinant très occidental
On ajoute encore 6° et ce cadran devient un cadran plein ouest. Du coup il rejoint la catégorie des cadrans polaires.
Internet
Les sites qui parlent de cadrans solaires sont très nombreux. Le site de Michel Lalos a été découvert par hasard. C'est un site très riche.
| Le site de Michel Lalos | |
| L'album des cadrans solaires français permet de retrouver le patrimoine, village par village. | |
| Ce que Michel Lalos rapporte du site de Tavel |